Project Goal

In this project, the participants will learn to model multiphoton multiple ionization dynamics of atoms exposed to intense x-ray radiation. The participants will evaluate crucial quantities and pulse-parameter dependencies that are relevant for high-intensity AMO experiments at XFEL sources. Such theoretical modelling is often applied at experiments where multiple x-ray ionization occurs, for example in Refs. [6, 4, 2, 1].

Preparations

You need to install the XATOM software, which is part of XRAYPAC. Please find instructions to download and install XRAYPAC on the website https://desy.de/~xraypac. The content of this exercise and all required files may be obtained from https://gitlab.desy.de/CDT/tutorialratesolving.git.

1 Rate Equation

The intense x-ray light in an XFEL pulse can ionize the sample many times. When molecules or atoms are exposed to such pulses, the overall dynamics can be modelled via sequential steps that describe a series of photoionization, Auger decay, and fluorescence processes. Such sequences (without fluorescence) are sketched in Fig. 1.

The involved multiphoton multiple ionization dynamics can be modeled to a good approximation via rate equations of the type

(1)

where p_i(t) is the time-dependent population of an electronic configuration i and γ_j→i(t) is a transition rate for a process between configuration j and i. In this exercise, we consider the following types of processes:

• Photoionization: The rate is given γ_j→i(t) = σ_j→iJ(t), i.e., the product of the corresponding photoionization cross section and photon flux J(t).
• Auger-Meitner decay: The rate is given by the corresponding Auger-Meitner decay rate γ_j→i(t) = Γ_j→i.
• Fluorescence: The rate is given by the corresponding fluorescence decay rate γ_j→i(t) = Γ_j→i.

Exercise 1

Motivation: Analytically solve the rate equation, derive dependecies for the competition of photoionization and Auger-Meitner decay.

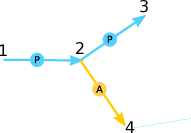
Given is the following set of rate equations:

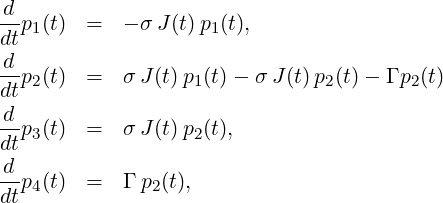
with the boundary conditions p₁(0) = 1, p₂(0) = 0, p₃(0) = 0, p₄(0) = 0, and a temporal step-function for the fluence,

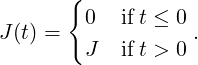This set of rate equations models the competition between Auger-Meitner decay and photoionization illustrated in Fig. 2: The ionization dynamics start with photoionization from electronic configuration 1 into configuration 2. Configuration 2 can either further be photoionized into configuration 4 (a PP sequence) or undergo Auger-Meitner decay into configuration 3 (a PA sequence). The possible pathways are also illustrated by the graph on the right hand side of the rate equation.

Give the analytical solution and plot them for varying parameters σJ and Γ. Help: For p₂(t), you may consider the ansatz p₂(t) = λ(t)exp(−(σJ + Γ)t). Alternatively, you may consider using the Laplace transformation. What is the probability to observe PP vs. PA process?

2 Calculate Decay Rates and Cross Sections

The transition rates for the electronic processes can be calculated using ab-initio methods. Here a short overview of the basic equations is given. See Ref. [3] for further details.

The photoionization cross section (in dipole approximation and assuming effectively independent electrons) is given by

(2)

where ω is the photon energy, E_f and E_i are the effective one-particle energies, ϕ_f and ϕ_i are the corresponding one-electron wavefunctions, 𝜖 is the polarization vector of the light field, and ∇ = (∂_x,∂_y,∂_z)^T .

Employing similar approximations on the electronic wave function, the Auger-Meitner decay rate from an initial electronic state with a core vacancy in orbital ϕ_c(r) (otherwise closed shell) and a final electronic state with two vacancies in ϕ_v1(r) and ϕ_v2(r) and an Auger-Meitner electron with continuum wave function ϕ_k(r) is given by

(3)

where

(4)

and E_v1, E_v2, E_c, and E_k are the corresponding one-particle energies.

The fluorescence rate is given by

(5)

where ω = E_i − E_f is the emitted fluorescence photon energy, and ⟨ϕ_f|r|ϕ_i⟩ is the transition dipole moment between the the initially occupied orbital ϕ_i and the initially vacant orbital ϕ_f.

The calculation of the respective transition rates can be a challenge on its own. They can be obtained by available electronic structure programs. In this course, we employ the atomic electronic structure program XATOM [5]. XATOM calculates transition rates employing the Hartree-Fock-Slates electronic structure model. All the obtained transition rates are average over the spin-angular terms for a given atomic configuration. For example, the cross section for core-shell ionization of a neutral, ground state carbon atom (configuration 1s²2s²2p²) is a weighted average over all the involved atomic terms ¹S, ³P, ¹D.

Exercise 2

Motivation: Learn how to use the electronic structure tool XATOM to calculate rates and cross-sections.

Exercise 2a

Make yourself familiar with the XATOM tool. You can calculate the electronic structure of a neon atom by typing

To calculate a specific electronic configuration of neon use

To calculate a photoionization cross section for a given photon energy use

Decay rates (for Auger-Meitner and fluorescence) can be calculated via

Moreover, you can get a short overview of command-line options with

Further usage is described in the pdf document “xatom_manual.pdf” in the project folder.

Exercise 2b

Calculate the photoionization cross section for neutral neon and ionized neon as a function of photon energy from 400 eV to 1000 eV. Plot the results (you may use any plot program you like).

Exercise 2c

Calculate the lifetime of core-ionized (configuration 1s¹2s²2p⁶), doubly core-coreionized (configuration 1s⁰2s²2p⁶) neon, and core and valence-ionized neon (e.g., configuration 1s¹2s²2p⁰). Compare the numbers. Can you explain why one is considerably larger?

3 Solve Rate Equations Numerically

The python notebook rateSolver.ipynb(html) contains a code for numerically solving rate equations. To solve the rate equations with this code, a table of rates and cross sections needs to be prepared that is fed into the numerical solver. The table for the previous 4-configuration example with parameters σ = 1, Γ = 3∕2, and J = 1 is already provided.

For neon, a table of rates and cross sections for a photon energy of 2 keV is also already provided. It has been generated with the python notebook tableGeneration.ipynb (html). Feel free to inspect it. You may also want to modify it to address other elements or further photon energies. In order to use it, you have to set XATOMPATH tp the path of your XATOM binary. Please consider that for larger atoms the number of electronic configurations explodes dramatically. For such atoms, solving the rate equation with tabulated rates thus becomes infeasible and other approaches have to be taken.

Exercise 3

Motivation: Learn how to solve the rate equations for a realistic scenario using numerical solver.

Exercise 3a

Modify the notebook to verify your previous analytical solution with the numerical one. Add the required code into blank cells in the notebook.

Exercise 3b

In the python notebook rateSolver.ipynb(html) the rate equations are solved for the provided table of rates and cross sections for neon. Make yourself familiar with the code. The variable nPhotonsperSqmuM specifies the number of photons per μm², the variable fwhmPulse specifies the full width at half maximum of the temporal pulse profile. Because of the many configurations involved, it is tedious to inspect the solution for every single configuration. Instead, the average charge is shown and the population of charge states (summing up the populations for configurations with the same charge state). The probability for PP vs. PA sequence is calculated as well. Try to change the parameters fluence and pulse duration and inspect how the results change.

Exercise 3c

Modify the notebook such that you generate plots of the average charge as a function of fluence and as a function of pulse duration. Add your code in the blank cells of the notebook. Plot the average final charge as a function of fluence for a given pulse duration. Plot the average final charge as a function of pulse duration for a given fluence. Plot the ratio of PP processes vs. PA processes as a function of fluence and pulse duration. Explain the observation.

Exercise 3d

Consider the notebook tableGeneration.ipynb (html). Can you do your analysis for another photon energy, e.g., 1 keV?

References