In most analyses signals for charm quarks have been obtained by
full reconstruction of the decay particles of the charmed hadrons
into which the quarks fragment. From the decay particles the invariant
mass is reconstructed, such that the number of signal events can be determined
from the resonance spectrum, above a non-resonant combinatorial background.
The reconstruction of the invariant mass works particularly
well in hadronic decays in which all final state particles are
measured as charged particles in the tracking detectors.
Calorimeter energy deposits are sometimes used for decay
channels containing ![]() or
or ![]() .
.
 |
The most widely used method to identify events containing charm is
the reconstruction of events in the so-called 'golden decay' channel,
in which the invariant mass of the ![]() meson is reconstructed in the
decay
meson is reconstructed in the
decay
![]() .
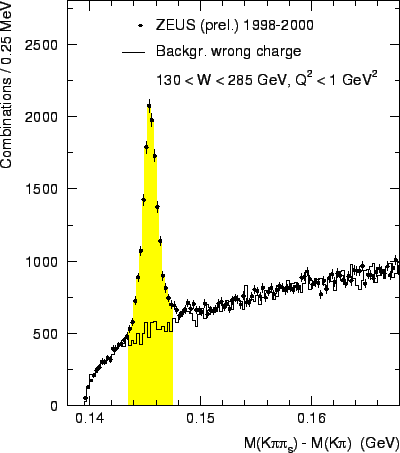
In fig.11 the difference
.
In fig.11 the difference ![]() between
the measured masses of the
between
the measured masses of the ![]() system and of the
system and of the ![]() meson decaying
into
meson decaying
into ![]() is shown. The number of signal events and the amount of
non-resonant background in the mass window is usually determined
by a fit to the signal and the side bands.
The width of the
is shown. The number of signal events and the amount of
non-resonant background in the mass window is usually determined
by a fit to the signal and the side bands.
The width of the ![]() peak is governed by the experimental resolution
of the pion track from the
peak is governed by the experimental resolution
of the pion track from the ![]() decay, as resolution effects from
the measurement of the two
decay, as resolution effects from
the measurement of the two ![]() decay particles largely
cancel in the subtraction. The
decay particles largely
cancel in the subtraction. The ![]() distribution is therefore
the preferred way to determine the number of
distribution is therefore
the preferred way to determine the number of ![]() mesons in the sample.
mesons in the sample.
The advantage of the full resonance reconstruction method is that all details
about the heavy quark resonance and decay kinematics are known and
the number of events can be determined precisely.
The disadvantage comes from small branching ratios,
![]() [144] and limited detector
capabilities such as finite detector acceptances and/or poor resolution.
At small
[144] and limited detector
capabilities such as finite detector acceptances and/or poor resolution.
At small ![]() the detector acceptance constrains measurements
in which samples of fully reconstructed
the detector acceptance constrains measurements
in which samples of fully reconstructed ![]() mesons are used
to about one third of the total phase space for charm
production [5].
Limited detector resolution leads to the need for
wide mass windows or large combinatorial background.
Bad resolution is a particular issue for
the identification and measurement of neutral particles at low energies
as neither experiment, H1 nor ZEUS, have been designed for this purpose.
mesons are used
to about one third of the total phase space for charm
production [5].
Limited detector resolution leads to the need for
wide mass windows or large combinatorial background.
Bad resolution is a particular issue for
the identification and measurement of neutral particles at low energies
as neither experiment, H1 nor ZEUS, have been designed for this purpose.