The determination of the charged particle momentum in HEP experiments
requires a fit of a parametrization to the points measured in a tracking
chamber. Various effects can result in deviations to the ideal helix
in the uniform field of a solenoid. One effect is multiple scattering,
which causes a random walk of the particle and affects especially
low-momentum tracks and very accurate measurements. The standard method
with a weight matrix, which includes the multiple scattering effects,
requires a solution time proportional to the third power of N, the number of
measured points, and has other disadvantages.
The track-fit algorithm based on broken lines is non-recursive and allows
to reconstruct the full particle trajectory taking into account details of
the multiple scattering. It provides optimal parameters and their
covariance matrices at track start and end, and optimal values
of the coordinates along
the trajectory including the variances. Allowing sparse-matrix techniques
the algorithm has an execution time proportional to N, the number of
measured points, and is under test conditions, a factor 10 faster than
the Kalman filter. The algorithm is explained in the Oxford and Zuerich
talks below.
The algorithm can be combined with robust techniques like the
least-median-of-squares and M-estimate methods, as explained in the DESY
Seminar talk. Using these techniques the algorithm can be used
effectively during track-finding and -recognition. The high speed of
the algorithm allows a fast rejection or down-weighting of outliers.
Another potential application is the fit of electron tracks, taking
effectively into account the photon radiation (Bethe-Heitler process).
This application is under study.
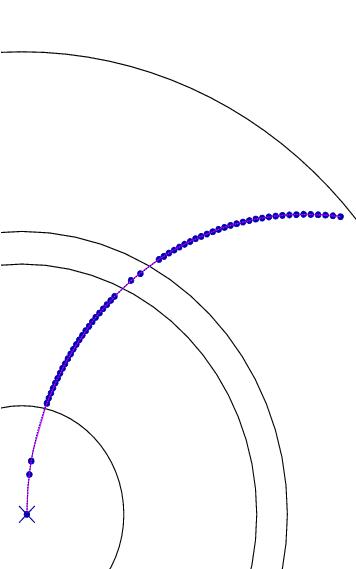
Hits on a track from a 200 MeV/c particle in a H1-like track detector is shown on the left. Visible are two hits of the accurate vertex detector, and many hits from the two driftchambers, with two (inaccurate) hits from the z-chamber between the two drift chambers (MC simulation).
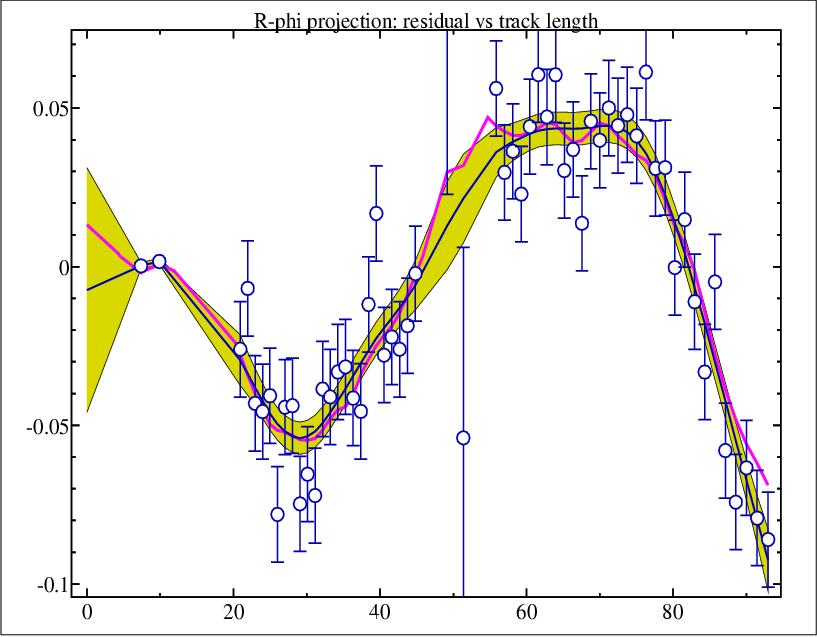
The residuals of the track hits with respect to a fitted circle are shown on the right as a function of the track length (all length in cm). The magenta line represents the true (MC) trajectory; visible are kinks, especially at the layers with a lot of material: beam pipe, vertex detector, inner and outer walls of the two drift chambers, z-chamber. The measured hits are shown with their errors. The blue line is the reconstructed trajectory with a straight line between each two reconstructed hit coordinates. The yellow band corresponds to +- 1 standard deviations, from the calculated errors of the reconstructed hit coordinates. The point at length zero is the extrapolated point at the vertex; its error is largely due to the material (beam pipe + wall) before the first measured hit. Reconstruction time including error calculation is about 1/10 of the Kalman filter time.