| (1) |
DOUBLE PRECISION FUNCTION Q2SIG(XPRIME,QLAM,KAPPA,LOOPFL,NF) - Instanton-induced hard subprocess total cross section
Calculation of
| (1) |
Q2SIG uses the form of the cross section derived in
Ref. [1],
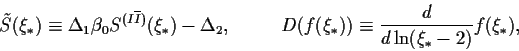 |
(5) |
The ![]() -action,
-action,
![]() , as well its
, as well its ![]() -derivatives,
entering the expression (2) for the cross section,
are calculated in the subroutine ACTION. For default settings of the
contrôl flags in QIINIT (VALFLAG=.TRUE.), it is given by the
exact valley form [2,3],
-derivatives,
entering the expression (2) for the cross section,
are calculated in the subroutine ACTION. For default settings of the
contrôl flags in QIINIT (VALFLAG=.TRUE.), it is given by the
exact valley form [2,3],
The fermionic overlap ![]() is calculated in the subroutine
OMEGA, which uses a simple but accurate approximation for the exact
result from Ref. [1],
is calculated in the subroutine
OMEGA, which uses a simple but accurate approximation for the exact
result from Ref. [1],
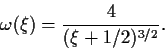 |
(11) |
The system (3) and (4) of saddle point equations is treated
as follows: In a first step, it is solved explicitly for ![]() in
terms of
in
terms of ![]() ,
,
The values of
![]() are calculated
in the subroutine XQS.
are calculated
in the subroutine XQS.
1999-08-21