In this subroutine1 an energy-weight factor
SUBROUTINE QIPSWT(PSWGT) - Generate kinematic weight for given phase space configuration
In this subroutine1 an energy-weight factor ![]() corresponding to the
leading-order matrix elements squared [1] is calculated: Each outgoing
quark with four-momentum
corresponding to the
leading-order matrix elements squared [1] is calculated: Each outgoing
quark with four-momentum ![]() is weighted by its energy
is weighted by its energy ![]() , each
outgoing gluon with four-momentum
, each
outgoing gluon with four-momentum ![]() by its energy squared
by its energy squared ![]() ,
such that
,
such that
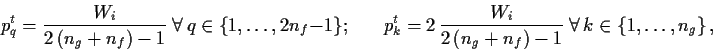 |
(2) |
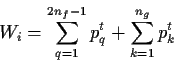 |
(3) |
![\begin{displaymath}
w_{\rm max}=2^{2\,n_g}
\left[ \frac{W_i}{2\,(n_g+n_f)-1}\right]^{2\,(n_g+n_f)-1} ,
\end{displaymath}](img9.gif) |
(4) |
| (5) |
1999-08-21