Up: QCDINS homepage Previous: Package description
DOUBLE PRECISION FUNCTION XI(XPR,XI_MIN,XI_MAX,XQ,XMU,NF,LOOPFL) -
Saddle point calculation of conformal ![]() -distance
-distance ![]()
In this routine the saddle point value of the conformal ![]() -separation
-separation
![]() is calculated as a function of
is calculated as a function of
![]() ,
,
![]() ,
,
![]() and
and ![]() .
The routine uses an interpolation in the range from
.
The routine uses an interpolation in the range from ![]() to
to
![]() to invert the relation
to invert the relation
![]() (see Eq. (9) below).
(see Eq. (9) below).
The system
of saddle point equations, with
is treated as follows:
In a first step, it is solved explicitly for ![]() in terms of
in terms of
![]() ,
,
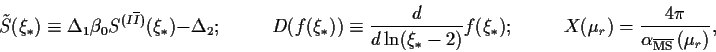 |
(6) |
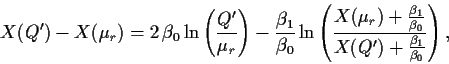 |
(7) |
In the second step, the expression Eq. (8) for ![]() is inserted
into
is inserted
into
In a last step, the solution
![]() can be
inserted into Eq. (8) to obtain
can be
inserted into Eq. (8) to obtain
![]() .
.
Up: QCDINS homepage Previous: Package description
1999-08-21
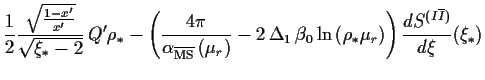
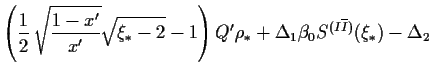

![\begin{displaymath}
v_\ast \equiv Q^\prime \rho_\ast
= 2\, D(\tilde{S})\,
W\le...
...}}{D(\tilde{S})}
\right]
\right\}}
{2\,D(\tilde{S})}
\right) ,
\end{displaymath}](img22.gif)