



Next: Proton Structure
Up: Theory
Previous: Theory
Contents
Perturbative Calculations
Perturbative QCD calculations can be performed in the formalism
of collinear factorization in which the DGLAP evolution
equations [59]
are used to describe the radiation of partons from the initial parton distribution in
the proton and in the photon.
In the collinear factorization ansatz the parton distributions in the
proton (and the photon) are assumed to depend only on the scaling
variable  and an energy scale
and an energy scale  , usually the photon virtuality
, usually the photon virtuality  .
In particular, the initial partons in the proton are assumed to carry no transverse
momentum. In the evolution, the partons are treated as massless on-shell particles.
Factorization and renormalization scale parameters are used to
absorb divergent parts of the perturbation series into parton distributions
and
.
In particular, the initial partons in the proton are assumed to carry no transverse
momentum. In the evolution, the partons are treated as massless on-shell particles.
Factorization and renormalization scale parameters are used to
absorb divergent parts of the perturbation series into parton distributions
and  .
In the DGLAP scheme, calculations up to next-to-next-to-leading
order (NNLO) have become available recently, e.g.for inclusive
cross sections [60].
.
In the DGLAP scheme, calculations up to next-to-next-to-leading
order (NNLO) have become available recently, e.g.for inclusive
cross sections [60].
In other approaches, such as the BFKL evolution
equation [61,62,63,64],
and later the CCFM evolution equation [65], the so-called  factorization formalism is used which is described
in section 2.5.
factorization formalism is used which is described
in section 2.5.
Heavy Quark production poses a particular theoretical challenge
as the presence of the heavy quark mass  or
or 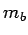 introduces a new scale into the perturbative calculations.
Quantitative calculations for heavy quark production at HERA have been
performed by a number of authors, providing detailed
results up to next-to-leading order in perturbation theory.
Predictions for inclusive heavy quark distributions, as derived from
fits to inclusive data from HERA and
fixed target experiments [66,67,68,69],
are available as a function of
introduces a new scale into the perturbative calculations.
Quantitative calculations for heavy quark production at HERA have been
performed by a number of authors, providing detailed
results up to next-to-leading order in perturbation theory.
Predictions for inclusive heavy quark distributions, as derived from
fits to inclusive data from HERA and
fixed target experiments [66,67,68,69],
are available as a function of  and
and  .
In global fits also other data, such as dijet data have been
used [70,71,72,73,74,75,76].
Predictions for exclusive processes in which the topologies of the two
quarks are explicitly taken into account, are available
as a function of a number of variables,
such as the transverse momenta
.
In global fits also other data, such as dijet data have been
used [70,71,72,73,74,75,76].
Predictions for exclusive processes in which the topologies of the two
quarks are explicitly taken into account, are available
as a function of a number of variables,
such as the transverse momenta  and/or pseudo-rapidity
and/or pseudo-rapidity
 for one or both of the heavy quarks and/or
jets (see section 2.1).
for one or both of the heavy quarks and/or
jets (see section 2.1).
Different schemes to calculate heavy quark production processes have
been developed in the framework of collinear factorization
which are expected to be valid in different kinematic
regions:
- In calculations for processes with light quarks, the mass of the
light quarks is assumed to be zero. The quarks are treated as
active partons in the proton, i.e.a density distribution for the
quarks in the proton is used to describe the non-perturbative
part of the calculation. The perturbative series is expanded
using a scale-parameter
 as given by the photon virtuality
as given by the photon virtuality  or the jet momentum
or the jet momentum  .
Perturbative calculations are expected to converge for
.
Perturbative calculations are expected to converge for
 .
Due to the heaviness of the quark mass
.
Due to the heaviness of the quark mass  , this approach
does not work for heavy quarks except in the extreme
limit
, this approach
does not work for heavy quarks except in the extreme
limit
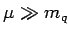 , in which the heavy quarks can be treated
as massless.
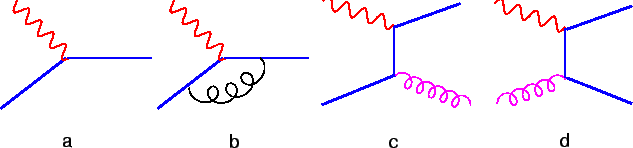
In this `massless' scheme, at leading order (LO), the quark parton
model (QPM) process (
, in which the heavy quarks can be treated
as massless.
In this `massless' scheme, at leading order (LO), the quark parton
model (QPM) process (
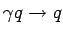 , fig. 2a)
is the dominant
contribution. At next-to-leading order (NLO), virtual corrections
are included (fig. 2b) and
the QCD Compton (
, fig. 2a)
is the dominant
contribution. At next-to-leading order (NLO), virtual corrections
are included (fig. 2b) and
the QCD Compton (
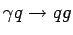 ,
fig. 2c) and
photon gluon fusion (
,
fig. 2c) and
photon gluon fusion (
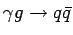 ,
fig. 2d)
processes also contribute.
The massless approach is often referred to as the zero mass variable flavor
number scheme (ZM-VFNS) [70,71].
In this approach the heavy quarks are treated as infinitely massive
below some scale
,
fig. 2d)
processes also contribute.
The massless approach is often referred to as the zero mass variable flavor
number scheme (ZM-VFNS) [70,71].
In this approach the heavy quarks are treated as infinitely massive
below some scale
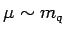 and massless above this threshold.
and massless above this threshold.
Figure 2:
Leading diagrams for heavy quark production in the massless scheme
at leading order (a) and next-to-leading order (b-d).
 |
- At values of
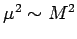 ,
the `massive' scheme [77,78,79],
in which the heavy flavor partons
are treated as massive quarks is more appropriate.
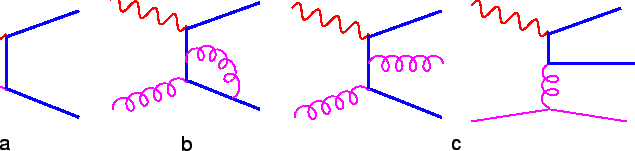
In the massive scheme the dominant LO process is photon
gluon fusion (PGF, fig. 3a) and
the NLO diagrams are of order
,
the `massive' scheme [77,78,79],
in which the heavy flavor partons
are treated as massive quarks is more appropriate.
In the massive scheme the dominant LO process is photon
gluon fusion (PGF, fig. 3a) and
the NLO diagrams are of order
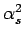 (figs. 3b-c).
The scheme is often referred to as the fixed flavor number scheme
(FFNS). As
(figs. 3b-c).
The scheme is often referred to as the fixed flavor number scheme
(FFNS). As 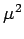 becomes large compared to
becomes large compared to 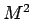 , the FFNS approach is
unreliable due to large logarithms in
, the FFNS approach is
unreliable due to large logarithms in
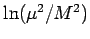 in the perturbative
series.
Generator programs in this scheme which are applicable to HERA physics
are available to next-to-leading order
(FMNR [80], HVQDIS [81]).
The fixed order massive scheme is also used in various
Monte Carlo event generator programs which implement
leading order matrix elements and parton showers to simulate higher
order effects. A description of these programs is given in
section 3.
in the perturbative
series.
Generator programs in this scheme which are applicable to HERA physics
are available to next-to-leading order
(FMNR [80], HVQDIS [81]).
The fixed order massive scheme is also used in various
Monte Carlo event generator programs which implement
leading order matrix elements and parton showers to simulate higher
order effects. A description of these programs is given in
section 3.
Figure 3:
Leading diagrams for heavy quark production in the massive scheme
at leading order (a) and next-to-leading order (b-d).
 |
- In order to provide reliable pQCD predictions for the description of
heavy flavor production over the whole range in
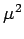 , composite
schemes which provide a smooth transition from the massive description
at
, composite
schemes which provide a smooth transition from the massive description
at
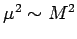 to the massless behavior at
to the massless behavior at
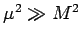 have been
developed.
These composite schemes are commonly referred to as
variable flavor number schemes (VFNS).
The VFNS approach has been incorporated in various different
forms to order
have been
developed.
These composite schemes are commonly referred to as
variable flavor number schemes (VFNS).
The VFNS approach has been incorporated in various different
forms to order  [82,83,84,85,75,86,87,88]
and to order
[82,83,84,85,75,86,87,88]
and to order
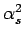 [89,90].
[89,90].
In resummed or `matched' next-to-leading-order QCD predictions
the divergent logarithms are controlled by
resummation techniques. Here, matched means that
measures are taken to avoid double-counting of contributions
which are contained in both the perturbative and the resummed part of the
calculation, i.e.
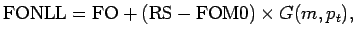 |
(2) |
where FONLL stands for fixed-order plus next to leading logarithms, and
FO is the fixed order,
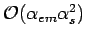 result.
RS is the resummed result, which includes all terms of the form
result.
RS is the resummed result, which includes all terms of the form
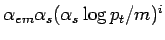 and
and
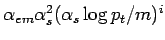 and neglects all terms suppressed by powers of the heavy quark mass
and neglects all terms suppressed by powers of the heavy quark mass 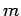 .
FOM0 is the massless limit of FO, in the sense that all terms suppressed
by powers of
.
FOM0 is the massless limit of FO, in the sense that all terms suppressed
by powers of 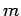 are dropped, while logarithms of the mass are retained;
thus FOM0 is the truncation of RS to order
are dropped, while logarithms of the mass are retained;
thus FOM0 is the truncation of RS to order
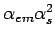 .
.
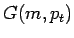 is an arbitrary dumping function, that must be regular
in
is an arbitrary dumping function, that must be regular
in  , and at large
, and at large  , it must approach unity up to terms
suppressed by powers of
, it must approach unity up to terms
suppressed by powers of 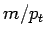 .
In the matched calculation FONLL [87,88,91,92,93] differential cross
sections are calculated to
next-to-leading-log precision using perturbative fragmentation
functions [94].
A similar approach is pursued in [95,96,97,98,99,100]. Here,
the ZM-VFNS is used as a starting point, adjusting the
factorization scales such that
the massive calculation is reached for
.
In the matched calculation FONLL [87,88,91,92,93] differential cross
sections are calculated to
next-to-leading-log precision using perturbative fragmentation
functions [94].
A similar approach is pursued in [95,96,97,98,99,100]. Here,
the ZM-VFNS is used as a starting point, adjusting the
factorization scales such that
the massive calculation is reached for
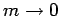 .
.




Next: Proton Structure
Up: Theory
Previous: Theory
Contents
Andreas Meyer
2006-02-13
![]() and an energy scale
and an energy scale ![]() , usually the photon virtuality
, usually the photon virtuality ![]() .
In particular, the initial partons in the proton are assumed to carry no transverse
momentum. In the evolution, the partons are treated as massless on-shell particles.
Factorization and renormalization scale parameters are used to
absorb divergent parts of the perturbation series into parton distributions
and
.
In particular, the initial partons in the proton are assumed to carry no transverse
momentum. In the evolution, the partons are treated as massless on-shell particles.
Factorization and renormalization scale parameters are used to
absorb divergent parts of the perturbation series into parton distributions
and ![]() .
In the DGLAP scheme, calculations up to next-to-next-to-leading
order (NNLO) have become available recently, e.g.for inclusive
cross sections [60].
.
In the DGLAP scheme, calculations up to next-to-next-to-leading
order (NNLO) have become available recently, e.g.for inclusive
cross sections [60].
![]() factorization formalism is used which is described
in section 2.5.
factorization formalism is used which is described
in section 2.5.
![]() or
or ![]() introduces a new scale into the perturbative calculations.
Quantitative calculations for heavy quark production at HERA have been
performed by a number of authors, providing detailed
results up to next-to-leading order in perturbation theory.
Predictions for inclusive heavy quark distributions, as derived from
fits to inclusive data from HERA and
fixed target experiments [66,67,68,69],
are available as a function of
introduces a new scale into the perturbative calculations.
Quantitative calculations for heavy quark production at HERA have been
performed by a number of authors, providing detailed
results up to next-to-leading order in perturbation theory.
Predictions for inclusive heavy quark distributions, as derived from
fits to inclusive data from HERA and
fixed target experiments [66,67,68,69],
are available as a function of ![]() and
and ![]() .
In global fits also other data, such as dijet data have been
used [70,71,72,73,74,75,76].
Predictions for exclusive processes in which the topologies of the two
quarks are explicitly taken into account, are available
as a function of a number of variables,
such as the transverse momenta
.
In global fits also other data, such as dijet data have been
used [70,71,72,73,74,75,76].
Predictions for exclusive processes in which the topologies of the two
quarks are explicitly taken into account, are available
as a function of a number of variables,
such as the transverse momenta ![]() and/or pseudo-rapidity
and/or pseudo-rapidity
![]() for one or both of the heavy quarks and/or
jets (see section 2.1).
for one or both of the heavy quarks and/or
jets (see section 2.1).
