Fehlerrechnung

Messfehler ein wenig anders. Jedes Messergebnis ist also nur eine Näherung des wahren Werts, oder anders gesagt: der gemessene Wert ist der wahre, gesuchte Wert mit einem bestimmten Fehler. Um mit den Messergebnissen sinnvoll arbeiten zu können, sollte dieser Fehler so klein wie möglich sein, das Messergebnis sollte so dicht wie möglich am wahren Wert liegen.

Die Schülerexperimente bei Cosmic@Web messen die Rate kosmischer Teilchen $R$, also die Anzahl gemessener Teilchen $N$ pro Zeiteinheit $t$:

Weil die Rate also von $N$ und $t$ abhängig ist, benutzt man zur Berechnung der Messabweichung $\Delta R$ das Fehlerfortpflanzungsgesetz (mehr Informationen dazu im Wikipedia-Artikel). Die Formel lautet für zwei unabhängige Größen, wie $N$ und $t$ es sind, folgendermaßen:

ist die Ableitung der Funktion nach $N$, das ist einfach . Analog dazu ist die Ableitung nach $t$, sie lautet . Das setzen wir ein und erhalten:

Weil der Computer die Zeit maschinell genau misst, ist die Zeitabweichung $\Delta t$ sehr klein. Dementsprechend ist das Quadrat davon $(\Delta t)$² fast 0 und somit vernachlässigbar. Es bleibt

Nun müssen wir noch $\Delta N$ bestimmen. Natürliche Prozesse wie das Herabprasseln kosmischer Teilchen lassen sich mit der Poisson- oder auch Gaußverteilung sehr gut beschreiben. Laut diesen mathematischen Gesetzen kann man für die Abweichung einsetzen. Nun wissen wir, wie groß die Abweichung der gemessenen Rate vom wahren Wert ist:

Daraus kann man auch bestimmen, wie lange man messen muss, um unter einem bestimmten Fehler zu bleiben. Die Messabweichung $\Delta R$ ist die Ungenauigkeit $x$ (in Prozent) vom wahren Wert $R$:

Diese Formel kann nun einfach nach $x$ umgestellt werden. Wir erhalten

Zuletzt wird noch nach der Zeit umgestellt:

Indem man nun die erwartete Rate für $R$ und einen bestimmten Fehler, den man erreichen möchte, für $x$ einsetzt, kann man sich die dafür nötige Messdauer $t$ ausrechnen. Grundsätzlich ist es immer sinnvoll so lange zu messen bis der Fehler unter 1% liegt. Wie viele Sekunden müsstest du dafür messen, wenn eine Rate von 6,67 Hz erwartet wird? Denke daran, dass die Einheit Hz=1/s ist und 1%=0,01.

Bei der Winkelmessung rechnet man in ähnlicher Weise. Kosmische Teilchen erreichen uns aus allen Richtungen. Die Rate, die wir für die einzelnen Richtungen erwarten, ist aber unterschiedlich. Die Rate ist abhängig vom Winkel $\alpha$, in dem man misst. Deswegen sieht die Formel für die Berechnung der Rate bei der Winkelmessung folgendermaßen aus:

Weil wir bei jeder anderen Messung den CosMO-Detektor einfach flach auf den Tisch legen, ist der Messwinkel dann $\alpha$=0. Mit cos(0)=1 ergibt das genau die vereinfachte Formel, die wir benutzt haben:

Bei der Winkelmessung hängt die Rate $R$ also gleich von drei Größen ab, die aber untereinander unabhängig sind: von der Anzahl $N$, der Zeit $t$ und dem Winkel $\alpha$. Diesmal lautet die Formel dementsprechend:

Auch hier vernachlässigen wir den Summanden mit der Zeit wieder, weil er fast 0 wird. Genauso ist die Winkeländerung fast 0, sodass auch dieser Term nicht weiter beachtet werden muss. Die Messabweichung ist also auch hier:

Die Ungenauigkeit in Prozent lautet mit der etwas anderen Formel für die Rate dann folgendermaßen:

und die Zeit, die man für einen bestimmten Fehler in einem Winkel messen muss, erhält man, indem man die Werte für die Rate $R$, den Fehler $x$ und den Messwinkel $\alpha$ in die nach $t$ umgestellte Formel einsetzt:

Bei einem Experiment ist das Ergebnis einer jeden Messung durch Messfehler ein wenig anders. Jedes Messergebnis ist also nur eine Näherung des wahren Werts, oder anders gesagt: der gemessene Wert ist der wahre, gesuchte Wert mit einem bestimmten Fehler. Um mit den Messergebnissen sinnvoll arbeiten zu können, sollte dieser Fehler so klein wie möglich sein, das Messergebnis sollte so dicht wie möglich am wahren Wert liegen.

Die Schülerexperimente bei Cosmic@Web messen die Rate kosmischer Teilchen $R$, also die Anzahl gemessener Teilchen $N$ pro Zeiteinheit $t$:

Weil die Rate also von $N$ und $t$ abhängig ist, benutzt man zur Berechnung der Messabweichung $\Delta R$ das Fehlerfortpflanzungsgesetz (mehr Informationen dazu im Wikipedia-Artikel). Die Formel lautet für zwei unabhängige Größen, wie $N$ und $t$ es sind, folgendermaßen:

ist die Ableitung der Funktion nach $N$, das ist einfach . Analog dazu ist die Ableitung nach $t$, sie lautet . Das setzen wir ein und erhalten:

Weil der Computer die Zeit maschinell genau misst, ist die Zeitabweichung $\Delta t$ sehr klein. Dementsprechend ist das Quadrat davon $(\Delta t)$² fast 0 und somit vernachlässigbar. Es bleibt

Nun müssen wir noch $\Delta N$ bestimmen. Natürliche Prozesse wie das Herabprasseln kosmischer Teilchen lassen sich mit der Poisson- oder auch Gaußverteilung sehr gut beschreiben. Laut diesen mathematischen Gesetzen kann man für die Abweichung einsetzen. Nun wissen wir, wie groß die Abweichung der gemessenen Rate vom wahren Wert ist:

Daraus kann man auch bestimmen, wie lange man messen muss, um unter einem bestimmten Fehler zu bleiben. Die Messabweichung $\Delta R$ ist die Ungenauigkeit $x$ (in Prozent) vom wahren Wert $R$:

Diese Formel kann nun einfach nach $x$ umgestellt werden. Wir erhalten

Zuletzt wird noch nach der Zeit umgestellt:

Indem man nun die erwartete Rate für $R$ und einen bestimmten Fehler, den man erreichen möchte, für $x$ einsetzt, kann man sich die dafür nötige Messdauer $t$ ausrechnen. Grundsätzlich ist es immer sinnvoll so lange zu messen bis der Fehler unter 1% liegt. Wie viele Sekunden müsstest du dafür messen, wenn eine Rate von 6,67 Hz erwartet wird? Denke daran, dass die Einheit Hz=1/s ist und 1%=0,01.

Bei der Winkelmessung rechnet man in ähnlicher Weise. Kosmische Teilchen erreichen uns aus allen Richtungen. Die Rate, die wir für die einzelnen Richtungen erwarten, ist aber unterschiedlich. Die Rate ist abhängig vom Winkel $\alpha$, in dem man misst. Deswegen sieht die Formel für die Berechnung der Rate bei der Winkelmessung folgendermaßen aus:

Weil wir bei jeder anderen Messung den CosMO-Detektor einfach flach auf den Tisch legen, ist der Messwinkel dann $\alpha$=0. Mit cos(0)=1 ergibt das genau die vereinfachte Formel, die wir benutzt haben:

Bei der Winkelmessung hängt die Rate $R$ also gleich von drei Größen ab, die aber untereinander unabhängig sind: von der Anzahl $N$, der Zeit $t$ und dem Winkel $\alpha$. Diesmal lautet die Formel dementsprechend:

Auch hier vernachlässigen wir den Summanden mit der Zeit wieder, weil er fast 0 wird. Genauso ist die Winkeländerung fast 0, sodass auch dieser Term nicht weiter beachtet werden muss. Die Messabweichung ist also auch hier:

Die Ungenauigkeit in Prozent lautet mit der etwas anderen Formel für die Rate dann folgendermaßen:

und die Zeit, die man für einen bestimmten Fehler in einem Winkel messen muss, erhält man, indem man die Werte für die Rate $R$, den Fehler $x$ und den Messwinkel $\alpha$ in die nach $t$ umgestellte Formel einsetzt:

Fitfunktionen

Oft ist es hilfreich, die experimentell gemessenen Daten durch eine mathematische Funktion zu beschreiben. Diese Modellierung des Versuchsergebnisses ermöglicht eine theoretische Untersuchung, Interpretation und Beschreibung der Zusammenhänge zwischen physikalsichen Größen. Aber es lassen sich nicht nur die aktuellen Messwerte charakterisieren. Eine passende Fitfunktion erlaubt auch Vorhersagen über das Verhalten der Daten, die über das Experiment hinausgehen.

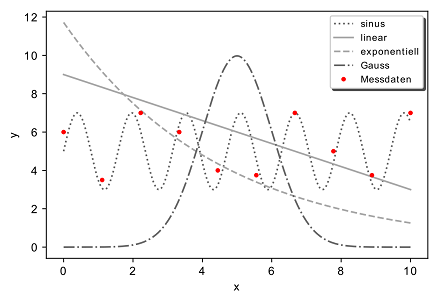
Die Anpassung einer Funktion zur Bestimmung ihrer Parameter wird im englischen Fit genannt. Häufig verwendete Fitfunktionen sind lineare, exponentielle, Gauß- und Sinus- bzw. Cosinus-Funktionen.

Forbush Decrease (FD)

Als FD wird der plötzliche Einbruch in der gemessenen kosmischen Strahlungsintensität bezeichnet. Er ist durch ein schnelles Absinken der Anzahl an gemessenen Teilchen und einen mehrere Tage dauernden Wiederaufstieg auf Normalniveau gekennzeichnet. Diese Einbrüche wurden erstmals von dem amerikanischen Physiker Scott E. Forbush in den 1930er und 1940er systematisch untersucht.

Verursacht werden FDs durch koronale Massenauswürfe. Dabei stößt die Sonne große Mengen an Plasma aus. Das Plasma kann man sich als eine Wolke vorstellen, die sich aus verschiedenen geladenen Teilchen (z.B. Ionen, Protonen) zusammensetzt. Da sich diese Teilchen beschleunigt durch den Raum bewegen, bilden sie ein Magnetfeld aus. Das Plasma schirmt durch sein mitgeführtes Magnetfeld andere geladene Teilchen ab.

Sonneneruptionen sind auch mit einer Schockwelle verbunden, die als Teilchenbarriere wirkt. Teilchen werden an dieser Schockwelle reflektiert, sodass hinter der Schockwelle die Teilchenanzahl geringer ist als davor.

Treffen Schockwelle und Plasma auf die Erde, kann ein zweistufiger FD beobachtet werden. Der erste Einbruch ist dabei durch die Schockwelle bedingt. Da sich hinter der Schockwelle weniger Teilchen befinden, können auf der Erde weniger Teilchen gemessen werden, wenn die Schockwelle auf die Erde trifft. Erreicht dann das Plasma die Atmosphäre der Erde, kommt es zu einem zweiten Einbruch, weil erneut weniger kosmische Teilchen die Erdoberfläche erreichen können. Dies ist aber nun durch das Magnetfeld des Plasmas verursacht, welches die kosmischen Teilchen von der Erde abschirmt. Das Plasma trifft also zeitlich versetzt auf die Erde und unterbricht die Rückkehr der Rate kosmischer Teilchen auf den Ausgangswert vor dem ersten Einbruch.

Im Allgemeinen wird die Rate kosmischer Teilchen als prozentuale Abweichung von einem Durchschnittswert dargestellt. Die Stärke eines FD wird dabei als die Differenz zwischen der Teilchenrate vor dem Ereignis und der Rate im Minimum ausgedrückt. Die Website spaceweather stellt Messwerte zu FDs seit 1957 zur Verfügung und kann bei der Suche nach FDs genutzt werden. Die Stärke eines FD wird mit Dmin angegeben und findet sich in der Tabelle. Für die Suche nach FDs in den Cosmic-Experimenten sollten nur sehr ausgeprägte Ereignisse ausgesucht werden. Als ausgeprägt gelten Ereignisse mit einem Wert von Dmin<-1.0.

Mehr Informationen zu FDs findest du im Wikipedia-Artikel.