Single Impact Parameter Method

Figure 15: Sketch of the impact parameter reconstruction. The sign of the impact parameter is based on the angle between the jet and the line between the primary vertex and the point of closest approach of the track. The two cases for a) a positive sign and b) a negative sign are shown.

In many analyses, a complete reconstruction of the heavy hadron invariant mass and/or displaced vertex is not possible - nor is it necessary, as the partial reconstruction and identification of event characteristics that signify the presence of heavy quarks, e.g.the presence of a leading lepton or decay lifetime distributions, is often sufficient for the measurement of heavy quark production cross sections and event distributions. The main advantage of those measurements in which heavy hadrons are only partially reconstructed, is that they can be performed on samples of much larger statistics. For example, in more recent measurements, the measured lifetime distributions have been used to determine the fraction of events containing charm and beauty (see section 5.5.2). For these measurements it is sufficient to measure at least one charged decay particle track in the silicon detectors from which the lifetime information is extracted.

The reconstruction of secondary detached vertices is experimentally demanding. An unambiguous association of all tracks to the secondary vertex can only be achieved if the spatial precision of the track measurement is of the same order as the distance between the primary and the secondary vertex, i.e. ${\cal O}(100\mu m)$. Harsh track selection cuts are necessary to ensure that the tracks fulfill this criterion, leading to a significant loss of statistics. For quantitative analyses of heavy quark production rates, e.g.cross section measurements, the loss of signal events due to lifetime-based selection cuts needs to be precisely estimated. This would require to precisely describe the track reconstruction efficiencies and the spatial resolutions of all tracks used for the reconstruction of the heavy hadron.

In recent analyses of the H1 Collaboration, a simpler method has been successfully used, which is based on the measurement of the impact parameters of one or several tracks, and thus allows to maintain a larger number of signal event candidates than the secondary vertex method. In the impact parameter method, only a subset of the tracks originating from the displaced vertex is used to perform a lifetime tag. The impact parameter of a track is defined as the transverse distance of closest approach (DCA) of the track to the primary vertex point. 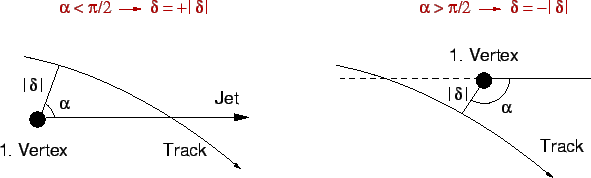The signed impact parameter $\delta$ (fig.15) of the charged particle track with respect to the primary event vertex reflects the lifetime of the particle from which the charged particle decays. The signed impact parameter is defined by reference to the direction of the reconstructed particle or the jet to which the track is associated. Usually, the direction is reconstructed using a jet algorithm (see above). The signed impact parameter of a track is defined as positive if the angle between the jet direction and the line joining the primary vertex to the point of DCA is less than $90^{\circ}$, and it is defined as negative otherwise (see fig.15). The sign allows to statistically disentangle detector resolution effects and effects from the decay lifetime of the heavy hadron. Tracks from the decays of long lived particles will have positive impact parameters, if resolution effects are neglected. Tracks produced at the primary vertex result in a symmetric distribution around 0, i.e.negative impact parameters predominantly result from detector resolution effects.

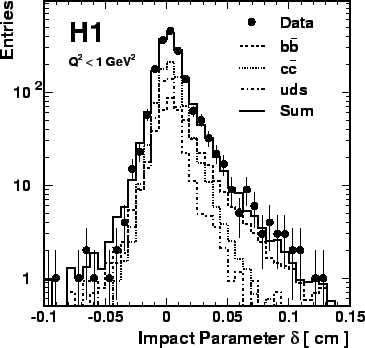
Figure 16 shows the distribution of the impact parameter of an identified muon track for a sample of photoproduction events with two or more jets and a muon [44]. In this sample the contribution from heavy quarks is enhanced by the requirement that a muon with transverse momentum $p_t> 2.5$ GeV be present. The lifetime effects are apparent in the asymmetric distributions of the estimated charm and beauty contributions. The normalization of the contributions has been determined by a fit to the data. Details of this analysis are described in section 6.2.1.

Figure 16: Distribution of the signed impact parameter of the muon track for a sample of photoproduction events with two jets and an identified muon. The solid line shows the distribution of the PYTHIA Monte Carlo simulation after a fit of the normalization of light quark, charm and beauty quark events [44].