Negative Subtraction Method

Figure: Significance distributions $S_1$ (a,b) and $S_2$ (c,d) before subtraction (a,c) and after subtraction (b,d) [43] (see text).

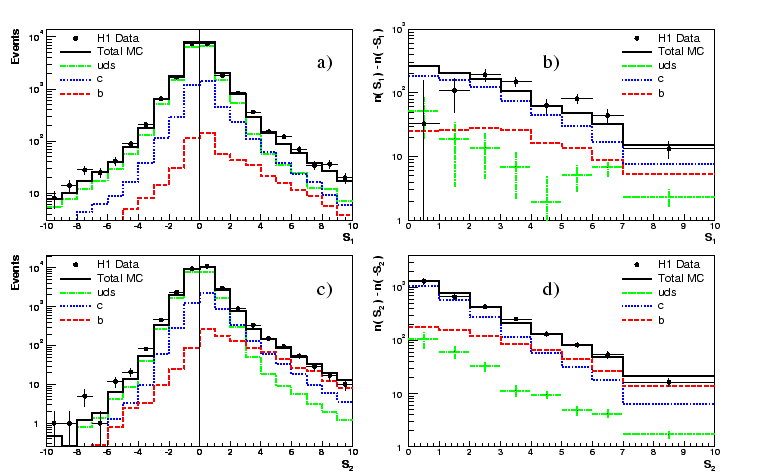
From the signed impact parameter a signed significance can be derived by dividing the measured signed impact parameter by the estimate of its resolution. Well measured tracks with large impact parameters lead to large values for the significance while badly measured tracks with large resolution remain in the core of the distribution. In fig.17 the significance distributions of tracks is shown for a sample of events at large photon virtualities $Q^2$[43]. A detailed description of the analysis based on such signatures is given in section 6.2.2. The selected tracks are required to have transverse momenta of larger than 500 MeV. No lepton or jet criteria are explicity imposed. Consequently, the relative contribution from charm and beauty events is significantly smaller than in fig.16.

Only those tracks with an impact parameter of less than 0.1 cm enter the significance distributions $S_1$ and $S_2$ (fig.17a and c). This selection suppresses contributions from decays of long lived particles containing strangeness and allows to achieve a reasonable discrimination of the charm and beauty components. Studies show that the significance distribution from strange particle decays is almost symmetric at small impact parameters. The distribution $S_1$ (fig.17a) denotes the significance of the track with the highest significance in the event. Only those events are used in which there is only one selected track. The significance $S_2$ (fig.17c) is defined for events with two or more selected tracks and where the track has the second highest significance of all selected tracks. In addition, it is required that the significance $S_2$ has the same sign as $S_1$ in the same event. The distributions are dominated by light quark events and exhibit large tails to both negative and positive values of significance with only a small asymmetry due to the long lived charm and beauty decays.

In the 'negative subtraction method' the negative bins in the significance distributions are mirrored at $S=0$ and subtracted from the positive. This way, effects that lead to significance distributions which are symmetric around zero are removed. In particular, the uncertainties due to the impact parameter resolution and the light quark normalization are substantially reduced.

The subtracted distributions are shown in figs.17b and d. The contributions from charm and beauty are determined by a fit which is performed simultaneously to both the subtracted $S_1$ and $S_2$ distributions and the total number of inclusive events before track selection. The shapes for the $c$, $b$ and $uds$ distributions are taken from Monte Carlo simulations and their normalization is fitted to the data. Only the statistical errors of the data and Monte Carlo simulation are considered in the fit. The Monte Carlo $c$, $b$ and $uds$ contributions in each $x$-$Q^2$ interval are allowed to be scaled by factors $P_c$, $P_b$ and $P_l$, respectively. The fit to the $S_1$ and $S_2$ distributions mainly constrains $P_c$ and $P_b$, whereas the overall normalization constrains $P_l$. The $c$ and $b$ quark fractions are distinguished in the fit by their different shapes in the $S_1$ and $S_2$ distributions.

The precise simulation of the simulated shapes is crucial for inclusive lifetime tag analyses. In particular, the size of the $b$-fraction obtained from the fits is directly dependent on the decomposition of the simulated charm sample into events with short-lived and with long-lived charmed hadrons (e.g.$D^{\pm}$), since the long-lived charmed hadrons have lifetime distributions and track multiplicities which are similar to those of beauty hadrons. In existing H1 analyses charm fragmentation universality is assumed and the fragmentation fractions as described in [159] are used which are based on measurements at LEP, CLEO and ARGUS. Measurements of charm fragmentation at HERA are discussed in detail in section 6.1.6.

Results consistent with the negative subtraction method have been found using alternative methods, such as the multi-impact parameter method (MIP) and the method of deterministic annealing.