Vertex detectors can be used to detect vertices displaced from the
primary interaction point. For charm mesons with lifetimes between 0.4
and 1 ps the typical spatial separation between their production vertex
and the decay vertex is given by their ![]() of 120 to 315
of 120 to 315 ![]() m.
m.
In a recent analysis at HERA, a complete
reconstruction of charmed mesons was performed in combination with
a lifetime tag to reduce the combinatorial backgrounds [6].
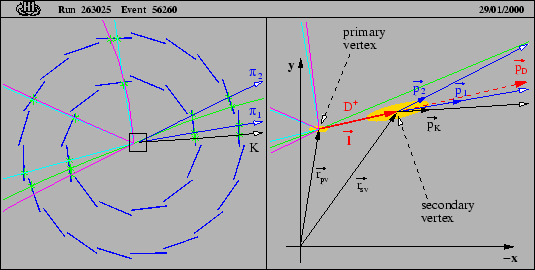
A sketch of the reconstruction procedure for the reconstruction
of the long-lived ![]() meson candidates
is shown in fig.13.
The main difficulty in the 3-body decays of the
meson candidates
is shown in fig.13.
The main difficulty in the 3-body decays of the ![]() into
into
![]() is the combinatorial background
which is large due to the large number of combinations of tracks
that can wrongly be assigned to one of the decay particles.
The signal-to-background ratio can drastically be improved
by use of a lifetime tag in which it is required that the tracks
originate from a common displaced vertex.
The vertex displacement is measured in the
is the combinatorial background
which is large due to the large number of combinations of tracks
that can wrongly be assigned to one of the decay particles.
The signal-to-background ratio can drastically be improved
by use of a lifetime tag in which it is required that the tracks
originate from a common displaced vertex.
The vertex displacement is measured in the ![]() -
-![]() plane.
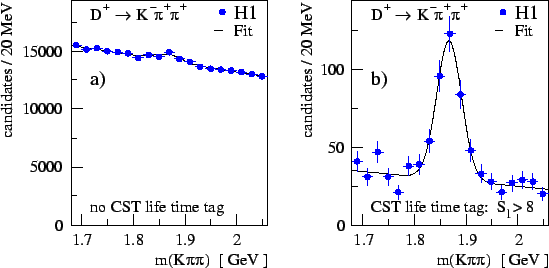
In fig.14 the mass spectrum is shown without and
with the cut
plane.
In fig.14 the mass spectrum is shown without and
with the cut ![]() on the vertex displacement.
Here,
on the vertex displacement.
Here, ![]() is the significance of the displacement, i.e. the distance
between the primary and secondary vertices divided by the uncertainty
of the distance measurement.
is the significance of the displacement, i.e. the distance
between the primary and secondary vertices divided by the uncertainty
of the distance measurement.
 |
 |