 |
 |
 |
At HERA, the dominant production channel for quarkonia with quantum
numbers of real photons (i.e.
![]() ) is through diffractive
processes.
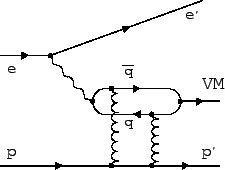
In perturbative QCD, the diffractive production of vector mesons can be
modeled in the proton rest frame by a process in which the photon
fluctuates into a
) is through diffractive
processes.
In perturbative QCD, the diffractive production of vector mesons can be
modeled in the proton rest frame by a process in which the photon
fluctuates into a ![]() pair at a long distance from the proton
target. The
pair at a long distance from the proton
target. The ![]() subsequently interacts with the proton via a
color-singlet exchange, i.e.in lowest order QCD via the exchange of a
pair of gluons with opposite color
(see fig.47)
[194,195,196,197,198,199,200].
At small
subsequently interacts with the proton via a
color-singlet exchange, i.e.in lowest order QCD via the exchange of a
pair of gluons with opposite color
(see fig.47)
[194,195,196,197,198,199,200].
At small ![]() , where
, where ![]() is the momentum-transfer-squared at the proton
vertex, the elastic process dominates, in which the proton stays intact.
Toward larger values of
is the momentum-transfer-squared at the proton
vertex, the elastic process dominates, in which the proton stays intact.
Toward larger values of ![]() , the dissociation of the proton into a
small-invariant-mass baryonic state becomes dominant.
Measurements of diffractive
vector-meson production cross sections and helicity structure from the
H1 [201,202,28,203,204,205,206,207,208] and
ZEUS [209,210,211,212,213,214,215,216,217] collaborations are available for
, the dissociation of the proton into a
small-invariant-mass baryonic state becomes dominant.
Measurements of diffractive
vector-meson production cross sections and helicity structure from the
H1 [201,202,28,203,204,205,206,207,208] and
ZEUS [209,210,211,212,213,214,215,216,217] collaborations are available for
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() production, spanning the ranges of
production, spanning the ranges of
![]() GeV
GeV![]() ,
,
![]() GeV
GeV![]() , and
, and
![]() GeV.
(
GeV.
(
![]() is the
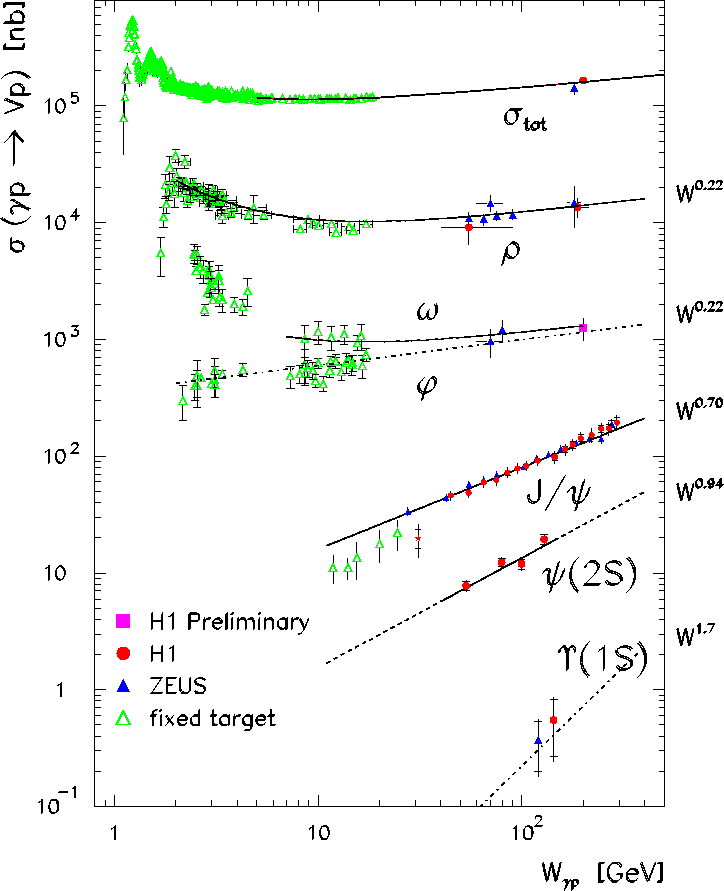
is the ![]() center-of-mass energy.) In
Figure 48, the elastic photoproduction cross
sections are shown.
Perturbative calculations in QCD are available for the kinematic
regions in which at least one of the energy scales
center-of-mass energy.) In
Figure 48, the elastic photoproduction cross
sections are shown.
Perturbative calculations in QCD are available for the kinematic
regions in which at least one of the energy scales ![]() (i.e.
(i.e. ![]() ,
,
![]() or
or ![]() ) is large and the strong-coupling constant
) is large and the strong-coupling constant
![]() is small [218,,,,,,].
is small [218,,,,,,].
In the presence of such a `hard' scale, QCD predicts a steep rise of the
cross section with
![]() . At small
. At small ![]() ,
, ![]() and meson
masses
and meson
masses ![]() , vector-meson production is known to show a
non-perturbative `soft' behavior that is described, for example, by
Regge-type models [225,226,227,228,229].
Toward larger values of
, vector-meson production is known to show a
non-perturbative `soft' behavior that is described, for example, by
Regge-type models [225,226,227,228,229].
Toward larger values of ![]() , in the leading logarithmic approximation,
diffractive
, in the leading logarithmic approximation,
diffractive ![]() production can be described by the effective
exchange of a gluonic ladder. At sufficiently low values of Bjorken-
production can be described by the effective
exchange of a gluonic ladder. At sufficiently low values of Bjorken-![]() (i.e. large values of
(i.e. large values of
![]() ), the gluon ladder is expected to
include contributions from BFKL
evolution [61,62,63,64,], as well as from DGLAP evolution [59,231].
), the gluon ladder is expected to
include contributions from BFKL
evolution [61,62,63,64,], as well as from DGLAP evolution [59,231].
The elasticity variable ![]() defined in equation (10)
is often used to demark
the boundary between the elastic and inelastic regions, with a typical
demarcation for
defined in equation (10)
is often used to demark
the boundary between the elastic and inelastic regions, with a typical
demarcation for ![]() production being
production being ![]() for the diffractive
region and
for the diffractive
region and ![]() for the inelastic region. However, at large
for the inelastic region. However, at large ![]() ,
there is actually no clear distinction between inelastic
,
there is actually no clear distinction between inelastic ![]() production and diffractive
production and diffractive ![]() production
in which the proton dissociates
into a final state with large invariant mass, owing to the fact that the
two processes can produce the same final-state particles.
In the region of large
production
in which the proton dissociates
into a final state with large invariant mass, owing to the fact that the
two processes can produce the same final-state particles.
In the region of large ![]() , both inelastic (section 6.4.1)
and diffractive production processes are expected to contribute to the cross section.
At the same time, calculations in perturbative QCD that assume a
diffractive color-singlet exchange are capable of describing the
production cross sections at large
, both inelastic (section 6.4.1)
and diffractive production processes are expected to contribute to the cross section.
At the same time, calculations in perturbative QCD that assume a
diffractive color-singlet exchange are capable of describing the
production cross sections at large
![]() [207,214,215].
A unified description in QCD
of the large
[207,214,215].
A unified description in QCD
of the large ![]() region, taking into account both inelastic and
diffractive contributions, is yet to be developed.
region, taking into account both inelastic and
diffractive contributions, is yet to be developed.