Next: Factorization
Up: Theory
Previous: Photon Structure
Contents
Fragmentation
In order to compare the calculations performed at parton level
with measurements of final states the fragmentation and hadronization
of the partons into hadrons have to be taken into account.
While the parton interactions are treated in perturbation theory,
the subsequent hadronization into measurable hadrons is usually
described by phenomenological models.
The transition from the heavy quark to a heavy hadron is
usually divided into two aspects:
- Fragmentation functions describe the transfer of the quark's energy to a
given hadron.
Many forms of fragmentation functions exist, the most prominent being
the Lund string model[105,106], as implemented
in the JETSET [107] and PYTHIA [108] Monte Carlo
event generators, and the
Peterson fragmentation function [109] which has the
form
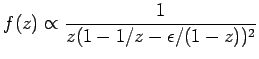 |
(4) |
where  is a free parameter.
The size of the parameter depends on the order of the
perturbative calculation. In leading order calculations it absorbs
effects that are contained in next-to-leading order calculations.
A number of alternative parameterizations
are available [110,111,112], some of which have
been seen to be successful in describing the LEP data.
In the parameterization by Kartvelishvili et
al. [113],
is a free parameter.
The size of the parameter depends on the order of the
perturbative calculation. In leading order calculations it absorbs
effects that are contained in next-to-leading order calculations.
A number of alternative parameterizations
are available [110,111,112], some of which have
been seen to be successful in describing the LEP data.
In the parameterization by Kartvelishvili et
al. [113],
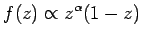 |
(5) |
and 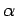 is an adjustable parameter.
The most precise measurements of the fragmentation parameters come
from experiments at
is an adjustable parameter.
The most precise measurements of the fragmentation parameters come
from experiments at  colliders
where the knowledge of the initial state kinematics provides
powerful constraint for these measurements and effects from interactions
between the final state and the beam
('beam drag' [114]) are absent.
colliders
where the knowledge of the initial state kinematics provides
powerful constraint for these measurements and effects from interactions
between the final state and the beam
('beam drag' [114]) are absent.
- Fragmentation ratios are used to describe the probability
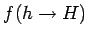 with which a heavy quark
with which a heavy quark 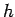 hadronizes to form a heavy hadron
hadronizes to form a heavy hadron 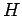 .
For charm hadrons the fragmentation ratios have been measured to great
accuracy at LEP [115,116] and these measurements have
generally been used
in measurements at HERA to determine the charm quark cross sections from
the measured rates of produced charmed hadrons.
Many of the Monte Carlo simulations (as described in section
3) have been tuned to the measured values.
Fragmentation ratios for higher excited states
of hadrons (such as
.
For charm hadrons the fragmentation ratios have been measured to great
accuracy at LEP [115,116] and these measurements have
generally been used
in measurements at HERA to determine the charm quark cross sections from
the measured rates of produced charmed hadrons.
Many of the Monte Carlo simulations (as described in section
3) have been tuned to the measured values.
Fragmentation ratios for higher excited states
of hadrons (such as  and
and  ) have only poorly been measured.
Recent measurements indicate that excited heavy
hadron states which subsequently decay via the strong interactions
into ground state hadrons are more copiously produced than previously
assumed [117].
The fragmentation function parameters obviously depend on the
assumed fragmentation ratio for these decays. Consequently,
analyses of these parameters need to take these correlations into account.
) have only poorly been measured.
Recent measurements indicate that excited heavy
hadron states which subsequently decay via the strong interactions
into ground state hadrons are more copiously produced than previously
assumed [117].
The fragmentation function parameters obviously depend on the
assumed fragmentation ratio for these decays. Consequently,
analyses of these parameters need to take these correlations into account.




Next: Factorization
Up: Theory
Previous: Photon Structure
Contents
Andreas Meyer
2006-02-13