



Next: Dijet Angular Distributions
Up: Open Charm Production
Previous: Inclusive Charm Production in
Contents
Charm Jet Cross Sections
The measurement of  mesons in events with dijets enhances
the sensitivity to higher order effects.
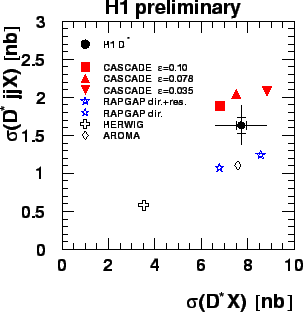
Figure 25 shows the H1 cross sections in the DIS regime for the
production of dijets in association with a
mesons in events with dijets enhances
the sensitivity to higher order effects.
Figure 25 shows the H1 cross sections in the DIS regime for the
production of dijets in association with a  meson versus the
meson versus the  meson
production cross section [8]. A transverse momentum of
at least 4(3) GeV is required for the highest (second highest)
meson
production cross section [8]. A transverse momentum of
at least 4(3) GeV is required for the highest (second highest)  jet, respectively.
The Monte Carlo simulations
RAPGAP, AROMA, CASCADE all reproduce the inclusive cross section but
do not describe the cross section of dijets in association with a
jet, respectively.
The Monte Carlo simulations
RAPGAP, AROMA, CASCADE all reproduce the inclusive cross section but
do not describe the cross section of dijets in association with a  meson.
While RAPGAP and AROMA (based on the DGLAP evolution equations)
are too low in normalization, the CASCADE Monte Carlo generator (based
on the CCFM equation) is too high.
HERWIG fails to describe the data for both the inclusive and the dijet
selection.
meson.
While RAPGAP and AROMA (based on the DGLAP evolution equations)
are too low in normalization, the CASCADE Monte Carlo generator (based
on the CCFM equation) is too high.
HERWIG fails to describe the data for both the inclusive and the dijet
selection.
In dijet processes the contribution from resolved processes can be measured.
The variable
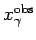 gives the energy fraction in the proton
rest frame, of the parton from the photon entering the hard subprocess.
It is reconstructed using the two highest transverse energy jets as
gives the energy fraction in the proton
rest frame, of the parton from the photon entering the hard subprocess.
It is reconstructed using the two highest transverse energy jets as
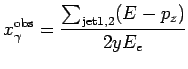 |
(6) |
where 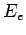 is the electron beam energy and
is the electron beam energy and  is the
photon inelasticity, i.e.the fractional electron energy carried by the
exchanged photon.
For the direct process (fig5a in
section 2.3),
is the
photon inelasticity, i.e.the fractional electron energy carried by the
exchanged photon.
For the direct process (fig5a in
section 2.3),
 approaches unity, as the hadronic final state consists of
only the two hard jets and the proton remnant in the
forward region. Energy depositions of the proton remnant in the forward direction contribute little to
approaches unity, as the hadronic final state consists of
only the two hard jets and the proton remnant in the
forward region. Energy depositions of the proton remnant in the forward direction contribute little to
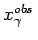 since
since
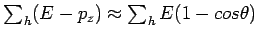 and
and
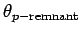 is close to 0.
In resolved processes (fig.5b-d in
section 2.3)
is close to 0.
In resolved processes (fig.5b-d in
section 2.3)
 can be small.
Other effects that lead to values of
can be small.
Other effects that lead to values of
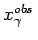 smaller than
unity are jet splitting, i.e.when two jets are reconstructed which
originate from the same mother parton, and higher order effects,
e.g.when hard gluons are radiated off the quarks.
smaller than
unity are jet splitting, i.e.when two jets are reconstructed which
originate from the same mother parton, and higher order effects,
e.g.when hard gluons are radiated off the quarks.
Figure:
The  dijet cross section versus the inclusive
dijet cross section versus the inclusive  cross section in comparison with various models [8].
The dijet cross sections as a function of
cross section in comparison with various models [8].
The dijet cross sections as a function of  of the leading jet
are shown in fig.60.
of the leading jet
are shown in fig.60.
 |
The ZEUS dijet photoproduction cross section [17]
as a function of
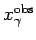 is shown in the figures 26a and b
compared with predictions
from PYTHIA [108], HERWIG [125]
and CASCADE [104], as well as a fixed order massive
calculation [80] in NLO QCD.
A significant part of the cross section is situated at low values of
is shown in the figures 26a and b
compared with predictions
from PYTHIA [108], HERWIG [125]
and CASCADE [104], as well as a fixed order massive
calculation [80] in NLO QCD.
A significant part of the cross section is situated at low values of
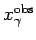 . In the approach of collinear factorization at
leading order this is consistent with the presence of resolved photon
processes.
. In the approach of collinear factorization at
leading order this is consistent with the presence of resolved photon
processes.
Figure:
Differential  dijet photoproduction cross sections
from ZEUS [17],
a)
dijet photoproduction cross sections
from ZEUS [17],
a)
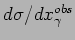 in comparison with Monte Carlo generators CASCADE, PYTHIA and HERWIG,
b)
in comparison with Monte Carlo generators CASCADE, PYTHIA and HERWIG,
b)
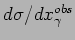 in comparison with
NLO FO predictions after hadronization correction (full lines)
and at parton level (dashed lines).
c-f)
in comparison with
NLO FO predictions after hadronization correction (full lines)
and at parton level (dashed lines).
c-f)
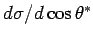 as a function of
as a function of
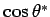 for the region of
for the region of
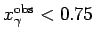 (resolved-enhanced, c and e) and
(resolved-enhanced, c and e) and
 (direct-enhanced, d and f) (see text).
Also shown are predictions from Monte Carlo generators (c and d) which
are individually scaled in normalization and from a NLO fixed order QCD calculation
(e and f). The dashed-dotted lines
show the jet-energy-scale uncertainty of the data.
(direct-enhanced, d and f) (see text).
Also shown are predictions from Monte Carlo generators (c and d) which
are individually scaled in normalization and from a NLO fixed order QCD calculation
(e and f). The dashed-dotted lines
show the jet-energy-scale uncertainty of the data.
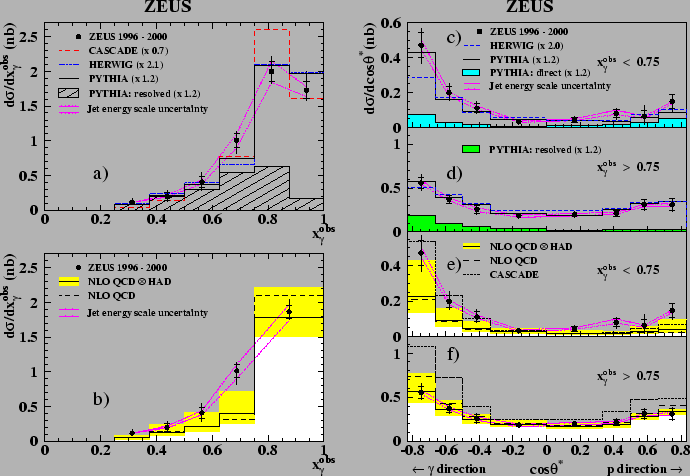 |




Next: Dijet Angular Distributions
Up: Open Charm Production
Previous: Inclusive Charm Production in
Contents
Andreas Meyer
2006-02-13
![]() mesons in events with dijets enhances
the sensitivity to higher order effects.
Figure 25 shows the H1 cross sections in the DIS regime for the
production of dijets in association with a
mesons in events with dijets enhances
the sensitivity to higher order effects.
Figure 25 shows the H1 cross sections in the DIS regime for the
production of dijets in association with a ![]() meson versus the
meson versus the ![]() meson
production cross section [8]. A transverse momentum of
at least 4(3) GeV is required for the highest (second highest)
meson
production cross section [8]. A transverse momentum of
at least 4(3) GeV is required for the highest (second highest) ![]() jet, respectively.
The Monte Carlo simulations
RAPGAP, AROMA, CASCADE all reproduce the inclusive cross section but
do not describe the cross section of dijets in association with a
jet, respectively.
The Monte Carlo simulations
RAPGAP, AROMA, CASCADE all reproduce the inclusive cross section but
do not describe the cross section of dijets in association with a ![]() meson.
While RAPGAP and AROMA (based on the DGLAP evolution equations)
are too low in normalization, the CASCADE Monte Carlo generator (based
on the CCFM equation) is too high.
HERWIG fails to describe the data for both the inclusive and the dijet
selection.
meson.
While RAPGAP and AROMA (based on the DGLAP evolution equations)
are too low in normalization, the CASCADE Monte Carlo generator (based
on the CCFM equation) is too high.
HERWIG fails to describe the data for both the inclusive and the dijet
selection.
![]() gives the energy fraction in the proton
rest frame, of the parton from the photon entering the hard subprocess.
It is reconstructed using the two highest transverse energy jets as
gives the energy fraction in the proton
rest frame, of the parton from the photon entering the hard subprocess.
It is reconstructed using the two highest transverse energy jets as
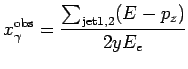

![]() is shown in the figures 26a and b
compared with predictions
from PYTHIA [108], HERWIG [125]
and CASCADE [104], as well as a fixed order massive
calculation [80] in NLO QCD.
A significant part of the cross section is situated at low values of
is shown in the figures 26a and b
compared with predictions
from PYTHIA [108], HERWIG [125]
and CASCADE [104], as well as a fixed order massive
calculation [80] in NLO QCD.
A significant part of the cross section is situated at low values of
![]() . In the approach of collinear factorization at
leading order this is consistent with the presence of resolved photon
processes.
. In the approach of collinear factorization at
leading order this is consistent with the presence of resolved photon
processes.
