 |
 |
Samples of charmed dijet events, where charm is identified
by the presence of a ![]() -meson
have been used to perform measurements of the
fragmentation functions [21,10].
The distributions are parameterized by fragmentation functions which
describe the transfer of the quark's energy to a given hadron
(see section 2.4).
Comparisons of the HERA measurements with data from experiments
at
-meson
have been used to perform measurements of the
fragmentation functions [21,10].
The distributions are parameterized by fragmentation functions which
describe the transfer of the quark's energy to a given hadron
(see section 2.4).
Comparisons of the HERA measurements with data from experiments
at ![]() colliders provide tests of the universality of
charm fragmentation.
colliders provide tests of the universality of
charm fragmentation.
At HERA, in contrast to ![]() colliders, the kinematics of
the initial boson-gluon state are not constrained such that the relative
hadron momentum must be determined solely from the measured
final state observables.
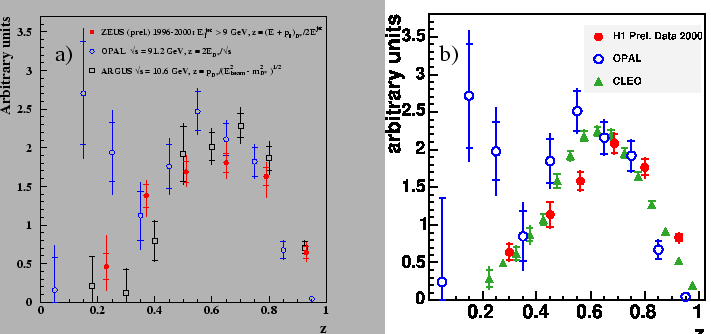
Figure 28 shows the acceptance corrected
distributions of the ZEUS and H1 charm dijet events
as a function of the fragmentation variable
colliders, the kinematics of
the initial boson-gluon state are not constrained such that the relative
hadron momentum must be determined solely from the measured
final state observables.
Figure 28 shows the acceptance corrected
distributions of the ZEUS and H1 charm dijet events
as a function of the fragmentation variable ![]() , which describes
momentum fraction carried by the
, which describes
momentum fraction carried by the ![]() meson relative to the
initial charm quark.
meson relative to the
initial charm quark.
In the case of ZEUS [21] (fig.28a)
photoproduction data with two jets of high transverse energy, ![]() GeV,
are used and the observable
GeV,
are used and the observable ![]() is reconstructed as
is reconstructed as
The H1 collaboration [10] (fig.28b) uses
an inclusive sample of ![]() mesons in DIS,
mesons in DIS, ![]() GeV
GeV![]() , with jets
of at least 3 GeV in transverse momentum, and also an alternative method
to reconstruct the observable
, with jets
of at least 3 GeV in transverse momentum, and also an alternative method
to reconstruct the observable ![]() .
In the hemisphere method, the projections of the particle momenta
perpendicular to the
.
In the hemisphere method, the projections of the particle momenta
perpendicular to the
![]() axis are calculated and
a thrust axis is found. The projected event is divided into two hemispheres,
one of them containing the
axis are calculated and
a thrust axis is found. The projected event is divided into two hemispheres,
one of them containing the ![]() meson and other hadrons.
meson and other hadrons.
![]() is then defined as
is then defined as
The ZEUS and H1 data show similar features as those from
OPAL [154], ALEPH [115],
ARGUS [155] and
CLEO [156] and reach a compatible precision.
The CLEO and ARGUS data are situated at a similar center-of-mass energy
of the ![]() -pair as those of H1, i.e.at
-pair as those of H1, i.e.at
![]() GeV,
while the OPAL and ALEPH data are significantly higher (
GeV,
while the OPAL and ALEPH data are significantly higher (
![]() GeV).
The OPAL data show a large contribution from gluon splitting
at small values of
GeV).
The OPAL data show a large contribution from gluon splitting
at small values of ![]() due to the large jet energy available at LEP.
The result supports the assumption of universality
of the charm fragmentation functions made in earlier measurements
and allows to improve the uncertainties due to fragmentation effects
for future measurements.
A fit of the ZEUS photoproduction data to the Peterson fragmentation
function [109] using the PYTHIA leading order
parton shower Monte Carlo generator and the Lund string
fragmentation model for lighter flavours [108] yields
a value for the Peterson fragmentation parameter
due to the large jet energy available at LEP.
The result supports the assumption of universality
of the charm fragmentation functions made in earlier measurements
and allows to improve the uncertainties due to fragmentation effects
for future measurements.
A fit of the ZEUS photoproduction data to the Peterson fragmentation
function [109] using the PYTHIA leading order
parton shower Monte Carlo generator and the Lund string
fragmentation model for lighter flavours [108] yields
a value for the Peterson fragmentation parameter
![]() [21].
The H1 DIS data [10] show a somewhat harder
[21].
The H1 DIS data [10] show a somewhat harder ![]() -spectrum and the
corresponding Peterson fragmentation parameter
is found to be
-spectrum and the
corresponding Peterson fragmentation parameter
is found to be
![]() , using the
same reconstruction of
, using the
same reconstruction of ![]() as ZEUS, which is based on reconstructed jets, as given in
equation (7).
For the hemisphere method, as given in equation (8),
a somewhat smaller value
as ZEUS, which is based on reconstructed jets, as given in
equation (7).
For the hemisphere method, as given in equation (8),
a somewhat smaller value
![]() is found.
For both analysis from ZEUS and H1, the determination of the fragmentation
functions in the framework of a next-to-leading order calculation is not yet available.
is found.
For both analysis from ZEUS and H1, the determination of the fragmentation
functions in the framework of a next-to-leading order calculation is not yet available.