CDTK.Interfaces.ForceField module

class CDTK.Interfaces.ForceField.forcefield(topol=None, **opts)

Bases: object

Template for a general force field

eAngles = 0.0

eBonds = 0.0

eCoul = 0.0

eDihdedral = 0.0

eNonbonbded = 0.0

getBonded(molX, topol)

input: molX: geometry of the molecule as flat numpy array topol: topology of the molecule

Output: energy,gradient energy: energy of bonded interaction gradient: gradient of the energy as flat numpy array

getCharges()

Returns array of charges for each atom / virtual site.

getConstraints(geom, der=False)

returns constraints

Input: geom: geometry of molecule, numpy array (natoms,3) der: (optionial) boolen Flag for wheter to provide dg as output

Output: if der, output is g,dg else, output is g

g: deviation in constraints, n-dim numpy array dg: derivative of constraints with respect to coordinates, numpy array of shape (n,na,3)

getLJCombRule()

returns the combination rule

getLJeps()

returns array of LJ epsilon parameter for each atom

getLJsigma()

returns array of LJ sigma parameter for each atom

getMasses()

Returns array of masses for each atom

getNonBondedInteractionPairs()

returns the atom pairs that experience non-bonded interaction (LJ + coulomb) within the molecule

getNonBondedInteractionPairsFudgeLJ()

returns the fudge factor non-bonded interaction (LJ) within the molecule

getNonBondedInteractionPairsFudgeQQ()

returns the fudge factor non-bonded interaction (Coulomb) within the molecule

getSigmaNuc(sigma_case)

Returns array with the spread (sigma) of the nuclear charge for each atom in a gaussian nuclear model. Sigma is parsed to the QCE.

ho(r) = Z_i * ( rac{1}{2 pi sigma_i^2})^(2/3) * exp(-r^2 / (2 sigma_i^2))

sigma_case: string or float, optional

If float, it is used as sigma for all atoms. If string, it can be either ‘covrad’, use the covalent radius of the atoms; or try to convert the string to a dictionary of the form {‘atom_name’: sigma_value}. Default is ‘covrad’.

sigma_nuc: (n_atoms,) ndarray of floats

getVGeom(geom, noM=False)

Input: geom: geometry as 2 dim numpy array geom[number of atoms, 3] noM: boolean, whether virtual sites for this molecule should be skipped

Output: vGeom, gM vGeom: geometry with virtual sites as 2 dim numpy array geom[number of atoms, 3] gM: Jacobi matrix elements as list ot tuples (ai,i,bj,j,g) ai: index of real atom i: index of atom coord (0…2) bj: index of virtual site j: index of virtual site coord (0…2) g: derviative dj / di

hasConstraints()

returns whether forcefield has constraints

hasVirtualSite()

returns True if forcefield has a virtual site logic

name()

returns the name of the force field

numConstraints()

returns number of constraints

class CDTK.Interfaces.ForceField.furfuralFF(topol=None, **opts)

Bases: forcefield

class CDTK.Interfaces.ForceField.jointForceFields(topol, LJCombRule='OPLS', waterForcefield=None, molecule2ffstr=None, **opts)

Bases: object

coulomb_egrad(dist_norm, dist_uvec, grad_shape, fudgeFactor)

Calculate the Coulomb interaction energy and gradient.

Parameters:

• dist_norm ((n_nonbonded) ndarray of floats.) – Norm of the distance between all pairs of atoms.

• dist_uvec ((n_nonbonded, 3)) – Unit vector between all pairs of atoms.

• grad_shape (tuple of int.) – Shape of the gradient (n_nuclei, 3)

• fudgeFactor ((n_nonbonded) ndarray of floats.) – Scaling factor for each non-bonded pair

Returns:

• energy_coul (float.) – Coulomb interaction energy.

• gradient_coul ((n_nuclei, 3) ndarray of float.) – Gradient of the Coulomb interaction energy.

enforceConstraints(x)

geomWithVirtualSites(geom, listNoM=[])

Function translates geometry into geometry with virtual sites that can be used for Coulomb calculation.

Parameters:

• geom ((n_atoms, 3) ndarray of floats.) – Positions of each atomic nuclei.

• listNoM (list, optional) – List of atom indices for which virtual sites should be skipped, by default []

Returns:

• vGeom ((n_atoms, 3) ndarray of floats.) – Geometry with virtual sites.

• vGeomD (list.) –

  List of elements of the Jacobian matrix between real and virtual geometry

  each element is a tuple (ai, i, aj, j, g), where:

  • ai: real geometry atomic index.

  • i: real geometry coordinate index 0…2.

  • aj: virtual geometry site index.

  • j: virtual geometry coordinate index 0…2.

  • g: derivative d r_j / d r_i.

getEnGrad(x, listNoM=[])

This subroutine calculates the energy and the gradient along all nuclear coordinates. At the moment is able to calculate the energy and the gradient of the following interactions:

• Bonded interactions

• Lennard-Jones interaction

• Coulomb interaction (deactivated for electrostatic embedding)

Parameters:

• x ((3 * n_atoms) ndarray of float.) – Coordinates of the nuclear centers.

• listNoM (list[int], optional) – Indices labeling the atoms for which virtual sites are disabled, by default []

Returns:

• energy (float.) – Energy given by the force field. Units are Hartree!

• gradient ((3 * n_atoms) ndarray of float.) – Gradient of the energy along all nuclear coordinates as flat numpy array. The order is as in the input. Units are Hartree/Bohr.

getRattleCorrection(vec0, vec1, dt, case='pos')

This method returns the correction to the position and velocity of a constrained geometry needed for the RATTLE algorithm. If case = “pos”, vec0 and vec1 represent r(t) and r(t+dt) without constraints, respectively. In this case, the correction to v(t+dt/2) is returned as it is needed to calculate r(t+dt) with constraints. If case = “vel” vec0 and vec1 represent r(t+dt) with constraints and v(t+dt) without constraints. In this case the correction to v(t+dt) with constraints is returned directly.

Parameters:

• vec0 ((3 * n_atoms) ndarray of float.) – r(t) [“pos”] or r(t+dt) [“vel”] without constraints applied.

• vec1 ((3 * n_atoms) ndarray of float.) – r(t+dt) [“pos”] or v(t+dt) [“vel”] with and without constraints applied, respectively.

• dt (float) – Timestep

• case (str, optional) – Flag to calculate correction to position [“pos”] or velocity [“vel”], by default “pos”

Returns:

correction – Correction to v(t+dt/2) [“pos”] or v(t+dt) [“vel”] for geometries with constraints.

Return type:

(n_atoms, 3) ndarray of float.

gradient_virt2orig(gradient, vGeomD)

This function translates gradient of virtual sites into gradient of original geometry.

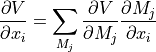
Parameters:

• gradient ((n_atoms, 3) ndarray of floats.) – Gradient at each virtual site position (some virtual positions are already real ones).

• vGeomD (list) –

  List of elements of the Jacobian matrix between real and virtual geometry each element is a tuple (ai, i, aj, j, g), where:

  • ai: real geometry atomic index.

  • i: real geometry coordinate index 0…2.

  • aj: virtual geometry site index.

  • j: virtual geometry coordinate index 0…2.

  • g: derivative d r_j / d r_i.

Returns:

grad_res – Gradient at each atom real position.

Return type:

(n_atoms, 3) ndarray of floats.

lennard_jones_egrad(dist_norm, dist_uvec, grad_shape, fudgeFactor)

Calculates the energy and gradient of the Lennard-Jones interaction.

Parameters:

• dist_norm ((n_nonbonded) ndarray of floats.) – Norm of the distance between all pairs of atoms.

• dist_uvec ((n_nonbonded, 3)) – Unit vector between all pairs of atoms.

• grad_shape (tuple of int.) – Shape of the gradient (n_nuclei, 3)

• fudgeFactor ((n_nonbonded) ndarray of floats.) – Scaling factor for each non-bonded pair

Returns:

• energy_LJ (float.) – Lennard-Jones interaction energy.

• gradient_LJ ((n_nuclei, 3) ndarray of float.) – Gradient of the Lennard-Jones interaction energy.

molecule2FF = {'SOL': <class 'CDTK.Interfaces.ForceField.waterFF_TIP4P2005f'>, 'UREA': <class 'CDTK.Interfaces.ForceField.ureaFF'>}

velWithVirtualSites(velocity, vGeomD)

This function translates velocities of original coordinates to velocities of virtual sites.

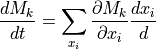
Parameters:

• velocity ((n_atoms, 3) ndarray of floats.) – Valocity of each virtual site position (some virtual positions are already real ones).

• vGeomD (list) –

  List of elements of the Jacobian matrix between real and virtual geometry each element is a tuple (ai, i, aj, j, g), where:

  • ai: real geometry atomic index.

  • i: real geometry coordinate index 0…2.

  • aj: virtual geometry site index.

  • j: virtual geometry coordinate index 0…2.

  • g: derivative d r_j / d r_i.

Returns:

vel_res – Velocity of virtual sites.

Return type:

(n_atoms, 3) ndarray of floats.

class CDTK.Interfaces.ForceField.ureaFF(topol=None, **opts)

Bases: forcefield

class CDTK.Interfaces.ForceField.waterFF_SPC(topol=None, **opts)

Bases: forcefield

class CDTK.Interfaces.ForceField.waterFF_SPCE(topol=None, **opts)

Bases: forcefield

class CDTK.Interfaces.ForceField.waterFF_TIP4P(topol=None, **opts)

Bases: forcefield

getVGeom(geom, noM=False)

Input: geom: geometry as 2 dim numpy array geom[number of atoms, 3] noM: boolean, whether virtual sites for this molecule should be skipped

Output: vGeom, gM vGeom: geometry with virtual sites as 2 dim numpy array geom[number of atoms, 3] gM: Jacobi matrix elements as list ot tuples (ai,i,bj,j,g) ai: index of real atom i: index of atom coord (0…2) bj: index of virtual site j: index of virtual site coord (0…2) g: derviative dj / di

For the TIP4P water molecule, the oxygen geometry is swapped with the geometry of the virtual site. Hydrogen positions in vGeom are identical to geom

hasVirtualSite()

returns True if forcefield has a virtual site logic

class CDTK.Interfaces.ForceField.waterFF_TIP4P2005(topol=None, **opts)

Bases: waterFF_TIP4P

class CDTK.Interfaces.ForceField.waterFF_TIP4P2005f(topol=None, **opts)

Bases: waterFF_TIP4P